Quadratures of the Circle by Exhaustion and by Indivisibles

Archimedes’ Quadrature of the Circle

When one seeks the area of some figure (in our case a circle), its quadrature involves finding a square (or other rectilinear figure) with the same area. An infinitary intuition might lead us to see the circle as a polygon with infinitely many sides: its circumference is made up of infinitely small linelets (i.e. segments whose lengths are not zero and yet smaller than any finite length). For each such linelet, consider the triangle formed by the two radii going from the end-points of the linelet to the center of the circle. The area of the circle is the “sum” of all these triangles, infinitely many of them (one for each infinitesimal linelet making up the circumference). Alternatively, we can think of the circle as obtained through the completion of an infinitary “limit process” starting from a square inscribed in the circle, and then successively inscribing other regular polygons with \(2^n\) sides. As \(n\) goes to infinity we approximate the area of the circle more and more and “completing” the process we reach the area of the circle.

Archimedes’ quadrature of the circle (just like other applications of exhaustion to other plane and solid figures) cleverly avoids these infinitary processes. Rather, Archimedes proceeds by considering the right triangle \(T\), one of whose sides is obtained by straightening out the circumference and whose other side is equal to the radius of the circle \(C\) whose quadrature is sought.

There are only three possibilities: \(C \lt T,\) \(C \gt T\) or \(C = T\) (here \(T\) and \(C\) refer with systematic ambiguity to the figures and their areas). Archimedes shows that the first and second possibility cannot hold by considering the differences \(T - C\) and \(C - T,\) respectively. In the first case, \(T - C\) is a non-zero area. Archimedes shows that one can find a circumscribed regular polygon \(P\) with \(2^n\) sides, for a specific \(n\), such that \(C \lt P \lt T\). Similarly, in the case that \(C - T\) is a non-zero area, he shows that one can find an inscribed regular polygon \(P\) with \(2^n\) sides, for a specific \(n\), such that \(T \lt P \lt C\). In both cases one reaches a contradiction in that the constructed polygons are such that \(T \lt P \lt T\) and \(P \lt T \lt P\), respectively.

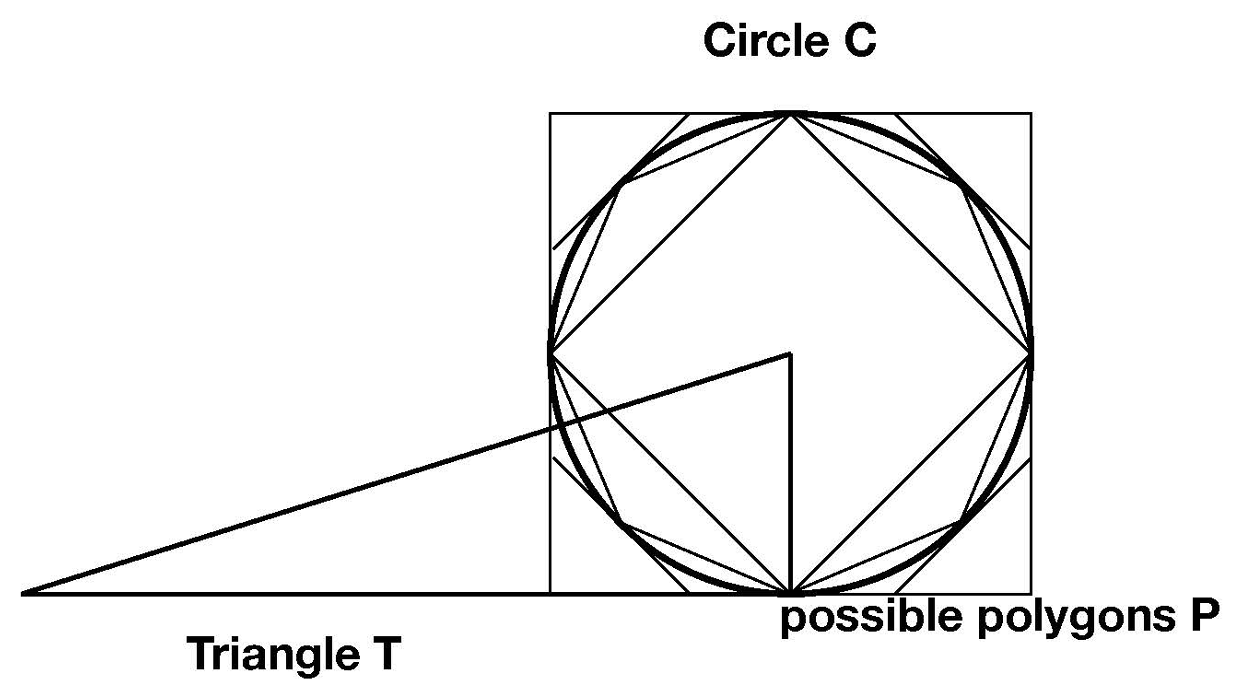
Figure 1.

Hence, \(C = T,\) the only possibility remaining. Essential here is that the “infinitary” intuitions have been replaced by finitary constructions. One only needs to construct finite regular polygons for the proof to go through.

Quadrature of the circle by indivisibles

Consider a square. Let the upper side move towards the lower side. All the parallel segments traced by the moving side are called the indivisibles of the figure. An indivisible of a plane figure is an element of lower dimension, such as a segment; the totality of the indivisibles in a way characterizes the figure.

Cavalieri’s “principle” (Cavalieri 1635) rested on the intuition that if two plane figures’ indivisibles have an invariant relation, then the areas themselves have that relation. We will illustrate this with an application to the quadrature of the circle given by Torricelli.

Consider the circle \(C\) and the triangle \(T\) as described in the Archimedean quadrature of the circle. Torricelli (1644), who extended Cavalieri’s theory to deal with curved indivisibles, considered the circle as being made up of infinitely many circumferences (the indivisibles of the circle) and the triangle of infinitely many segments (the indivisibles of the triangles). In addition, he paired each circumference of \(C\) with one and only one segment of \(T\) so that the ratio of the two was always 1:1. By Cavalieri’s principle, he concluded that the area of the circle is equal to that of the triangle. The figure illustrates the case with IO an arbitrary indivisible of the circle DB and IL the corresponding indivisible of the triangle (each point along AB determines one indivisible of the circle and the corresponding indivisible of the triangle ABC).

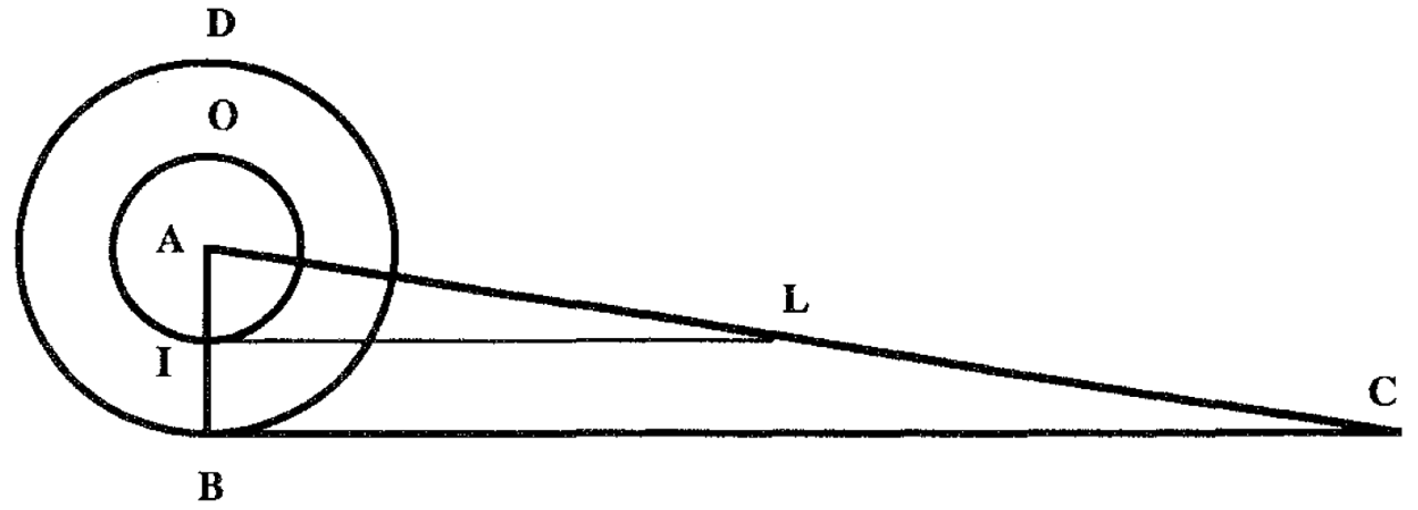
Figure 2.