Supplement to Hermann Weyl
Weyl’s metric-independent construction of the symmetric linear connection
Weyl characterizes the notion of a symmetric linear connection as follows:
Definition A.1 (Affine Connection)
Let \(T(M_{p})\) denote the tangent space of \(M\) at \(p \in M\). A
point \(p \in M\) is affinely connected with its immediate
neighborhood, if and only if for every vector \(v_{p} \in T(M_{p})\),
a vector at \(q\)
is determined to which the vector \(v_{p} \in T(M_{p})\) gives rise under parallel displacement from \(p\) to the infinitesimally neighboring point \(q\).
Of the notion of parallel displacement, Weyl requires that it satisfy the following condition.
Definition A.2 (Parallel Displacement)
The transport of a vector \(v_{p} \in T(M_{p})\) to an infinitesimally
neighboring point \(q \in M\) constitutes a parallel displacement if
and only if there exists a coordinate system \(\overline{x}^{i}\)
(called a geodesic coordinate system) for the neighborhood of
\(p \in M\), relative to which the transported vector
\(\overline{v}_{q}\) possesses the same components as
\(\overline{v}_{p}\); that is,
The requirement that there exist a geodesic coordinate system such that (45) is satisfied, characterizes the essential nature of parallel transport.
It is natural to require that for an arbitrary coordinate system the components \(dv^{i}_{p}\) in (44) vanish whenever \(v^{i}_{p}\) or \(dx^{i}_{p}\) vanish. Hence, the simplest assumption that can be made about the components \(dv^{i}_{p}\) is that they are linearly dependent on the two vectors \(v^{i}_{p}\) and \(dx^{i}_{p}\). That is, \(dv^{i}_{p}\) must be bilinear in \(v^{i}_{p}\) and in \(dx^{i}_{p}\); that is,
\[\tag{46} dv^{\,i}_{p} = - \Gamma^{i}_{jk}(x)v^{\,j}_{p}dx^{k}_{p}, \]where the \(n^{3}\) coefficients \(\Gamma^{i}_{jk}\)(x) are coordinate functions, that is functions of \(x^{i}\) \((i = 1, \ldots ,n)\), and the minus sign is introduced to agree with convention.
The \(v^{\,j}_{p}\) and \(dx^{k}_{p}\) in (46) are vectors, but \(dv^{\,i}_{p} = v^{\,i}_{q} - v^{\,i}_{p}\) is not a vector since the vectors \(v^{\,i}_{q}\) and \(v^{\,i}_{p}\) lie in different tangent planes and cannot be subtracted. Hence the coefficients \(\Gamma^{i}_{jk}(x)\) do not constitute a tensor; they conform to a linear but non-homogeneous transformation law. The vector
\[ v^{\,i}_{q} = v^{\,i}_{p} + dv^{\,i}_{p} = v^{\,i}_{p} - \Gamma^{i}_{jk}v^{\,j}_{p}dx^{k}_{p} \]is called the parallel displaced vector.
Weyl (1918b, 1923b) proves the following theorem.
Theorem A.3
If for every point \(p\) in a neighborhood \(U\) of \(M\), there
exists a geodesic coordinate system \(\overline{x}\) such that the
change in the components of a vector under parallel transport to an
infinitesimally near point \(q\) is given by
then locally in any other coordinate system \(x\),
\[\tag{48} dv^{\,i}_{p} = - \Gamma^{i}_{jk}(x)v^{\,j}_{p}dx^{k}_{p}, \]where \(\Gamma^{i}_{jk}(x) = \Gamma^{i}_{kj}(x)\), and conversely.
The idea of parallel displacement leads immediately to the idea of the covariant derivative of a vector field. Consider a vector field \(v^{i}(x)\) evaluated at two nearby points \(p\) and \(q\) with arbitrary coordinates \(x^{i}\) and \(x^{i} + \delta x^{i}\) respectively. A first-order Taylor expansion yields
\[\tag{49} u^{\,i}_{q} = v^{\,i}_{p}(x + \delta x) = v^{\,i}_{p}(x) + \frac{\partial v^{\,i}}{\partial x^{\,j}} \delta x^{\,j}_p . \]If we set
\[\tag{50} \frac{\partial v^{\,i}}{\partial x^{\,j}} \delta x^{\,j}_p = \delta v^{\,i}_p(x), \]then
\[\tag{51} \delta v^{\,i}_{p}(x) = v^{\,i}_{p}(x + \delta x) - v^{\,i}_{p}(x), \]and
\[\tag{52} u^{\,i}_{q} = v^{\,i}_{p} + \delta v^{\,i}_{p}. \]The array of derivatives
\[ \frac{\partial v^{\,i}}{\partial x^{\,j}} \]do not constitute a tensorial entity, because the derivatives are formed by the inadmissible procedure of subtracting the vector \(v^{\,i}_{p}(x)\) at \(p\) from the vector \(u^{\,i}_{q} = v^{\,i}_{p}(x + \delta x)\) at \(q\). Their difference \(\delta v^{\,i}_{p}(x)\) is not a vector since the vectors lie in the different tangent spaces \(T(M_{p})\) and \(T(M_{q})\), respectively. Since \(\delta x^{\,i}_{p}\) is a vector whereas \(\delta v^{\,i}_{p}\) is not, the array of derivatives
\[ \frac{\partial v^{\,i}}{\partial x^{\,j}} \]in (50) cannot therefore be a tensorial entity. To form a derivative that is tensorial, that is covariant or invariant, we must subtract from the vector \(u^{\,i}_{q} = v^{\,i}_{p} + \delta v^{\,i}_{p}\) not the vector \(v^{\,i}_{p}\), but another vector at \(q\) which “represents” the original vector \(v^{\,i}_{p}\) as “unchanged” as we proceed from \(p\) to \(q\). Such a representative vector at \(q\) may be obtained by parallel transport of the vector \(v^{\,i}_{p}\) to the nearby point \(q\), and will be denoted, given an arbitrary coordinate system \(x\), by
\[\tag{53} v^{\,i}_{q} = v^{\,i}_{p} + dv^{\,i}_{p}\,. \]Since \(dv^{\,i}_{p}\) is the difference between \(v^{\,i}_{p}\) and \(v^{\,i}_{q}\), \(dv^{\, i}_{p}\) is also not a vector for the for the reasons given above; however, the difference
\[\begin{align} u_{q} - v_{q} &= v^{\,i}_{p} + \delta v^{\,i}_{p} - [v^{\,i}_{p} + dv^{\,i}_{p}] \\ \tag{54} &= \delta v^{\,i}_{p} - dv^{\,i}_{p} \end{align}\]is a vector and is therefore a tensorial entity.
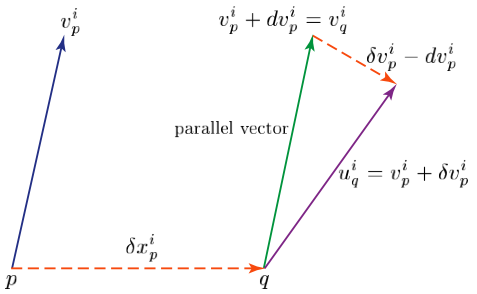
Figure 16: Covariant differentiation
The covariant derivative can now be defined by the limiting process
\[\begin{align} \nabla_{k}v^{\,i}_{p} &= \lim_{\delta x^{k}_{p} \rightarrow 0} \frac{(v^{\,i}_{p} + \delta v^{\,i}_{p} - v^{\,i}_{p} - dv^{\,i}_{p})}{\delta x^{k}_{p}} \\ \tag{55} &= \lim_{\delta x^{k}_{p} \rightarrow 0} \frac{(\delta v^{\,i}_{p} - dv^{\,i}_{p})}{\delta x^{k}_{p}} \\ &= \frac{\partial v^{\,i}_p}{\partial x^k} + \Gamma^i_{jk} v^{\,j}_{p}. \end{align}\]In general, one writes the covariant derivative of a vector field \(v^{i}\) simply as
\[\tag{56} \nabla_{k}v^{\,i} = \partial_{k}v^{\,i} + \Gamma^{i}_{jk}v^{\,j}. \]Weyl (1918b, §3.I.B) also provided a more synthetic argument to establish the symmetry of the affine connection. He considers two infinitesimal vectors \(\overline{PP}_{1}\) and \(\overline{PP}_{2}\) at a point \(P\). The vector \(\overline{PP}_{1}\) under parallel transport along \(\overline{PP}_{2}\) goes into \(\overline{P_{2}P}_{21}\). Similarly, the vector \(\overline{PP}_{2}\) under parallel transport along \(\overline{PP}_{1}\) goes into \(\overline{P_{1}P}_{12}\). These relationships are illustrated in figure 17.
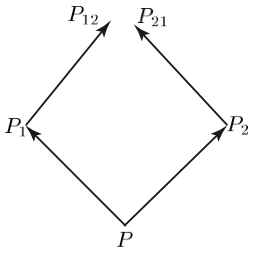
Figure 17: Symmetry of Parallel Transport
The condition imposed on parallel transport is that the four vectors \(\overline{PP}_{1}\), \(\overline{P_{1}P}_{12}\), \(\overline{PP}_{2}\) and \(\overline{P_{2}P}_{21}\) form a closed parallelogram; that is, the points \(P_{12}\) and \(P_{21}\) coincide. It follows that
\[\tag{57} \overline{PP}_{1} + \overline{P_{1}P}_{12} = \overline{PP}_{2} + \overline{P_{2}P}_{21}. \]Denote the coordinates of \(\overline{PP}_{1}\) and \(\overline{PP}_{2}\) by \(dx^{i}\) and \(\delta x^{i}\), respectively. The coordinates of \(\overline{P_{2}P}_{21}\) and \(\overline{P_{1}P}_{12}\) are respectively denoted by \(dx^{i} + \delta dx^{i}\) and \(\delta x^{i} + d\delta x^{i}.\) Substitution into (57) yields
\[\tag{58} dx^{i} + \delta x^{i} + d\delta x^{i} = \delta x^{i} + dx^{i} + \delta dx^{i}, \]or
\[\tag{59} d\delta x^{i} = \delta dx^{i}. \]From the assumption that the vectors transform linearly, one has
\[\tag{60} \begin{matrix} \delta dx^{i} = - \delta \gamma^{i}_{r}dx^{r} & \text{and} & d\delta x^{i} = - d\gamma^{i}_{r}\delta x^{r} \end{matrix}\]From the assumption that the infinitesimal transformation coefficients \(\delta \gamma^{i}_{r}\) and \(d\gamma^{i}_{r}\) are of the same order as the corresponding differentials \(\delta x^{i}\) and \(dx^{i}\), one obtains
\[\tag{61} \begin{matrix} \delta \gamma^{i}_{r} = \Gamma^{i}_{rs}\delta x^{s} & \text{and} & d\gamma^{i}_{r} = \Gamma^{i}_{rs}dx^{s}. \end{matrix}\]Substitution of (60) and (61) into (59) yields
\[\tag{62} \Gamma^{i}_{jk} = \Gamma^{i}_{kj} \]